Uji Normalitas Data dengan SPSS

Artikel sebelumnya adalah Uji Reliabilitas. Seperti kata dasarnya, uji normalitas dilakukan untuk mengetahui apakah data tersebut mengikuti distribusi normal atau tidak. Uji normalitas merupakan bagian dari uji persyaratan analisis statistik atau analisis uji asumsi dasar. Uji asumsi dasar adalah syarat yang harus dipenuhi sebelum data yang ada di uji dengan uji statistik yang sesungguhnya. Uji ini biasanya menggunakan data yang berskala ordinal, interval atau rasio. Jika data tidak berdistribusi normal dan atau jumlah sampel sedikit dan jenis data adalah nominal atau ordinal, maka metode yang digunakan adalah statistik non parameterik. Untuk uji kenormalan dari sampel dapat dilakukan dengan bantuan Uji Shapiro-Wilk, Kolmogrov-Smirnov dan Liliefors serta gambar normal Probability Plots.

Dasar pengambilan keputusan dalam uji normalitas adalah:

1. Jika Sig. (Signifikansi) atau nilai probabilitas < 0,05, maka data berdistribusi tidak normal.
2. Jika Sig. (Signifikansi) atau nilai probabilitas > 0,05, maka data berdistribusi normal.

Dalam kesempatan kali ini saya akan menggunakan Uji Normalitas yang dilakukan dengan bantuan Uji Shapiro-Wilk. Adapun data yang di uji adalah kenormalan Partisipasi anggota dalam pemilihan ketua IPM dengan Kepercayaan (trust) pada calon ketua.  

Langkah-langkahnya sebagai berikut.

1. Buka lembar kerja baru Program SPSS.

2. Klik Variable View pada SPSS Data Editor.

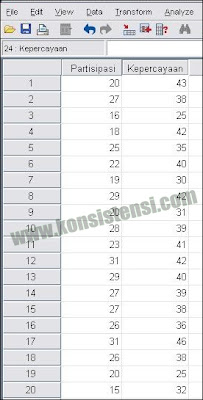
3. Tuliskan nama dengan kata dasar variabel atau dengan X dan Y, Decimals ganti dengan 0, Label isi dengan nama lengkap variabel, kemudian klik Data View, sehingga tampilanya seperti di bawah ini.

Tapilan pada Variable View

Tampilan pada Data View

4. Dari menu utama SPSS, pilih menu Analyze, kemudian pilih submenu Deskriptive Statistiks.

5. Dari serangkaian yang ada, pilih Explore, maka akan muncul dialog Explore.

6. Dependen List, Klik variabel Partisipasi anggota dalam pemilihan ketua IPM, kemudian klik tanda bagian yang atas.

7. Factor List, Klik variabel Kepercayaan (trust) pada calon ketua, kemudian klik tanda panah.

8. Klik pilihan Statistiks, pilih Deskriptive, lalu klik Continue.

9. Klik pilihan Plots, pada bagian Boxplot pilih None. Pada Deskriptive, Pilih Strem and leaf.

10. Klik pilihan Normality Plot With Tests.

11. Pada pilihan Spread vs Level With Levene Test, pilih Power Estimation, kemudian klik Continue.

12. Pada bagian Displays, pilih Both (yang artinya statistiks maupun Plots akan digunakan).

13. Klik OK jika seuma sudah selesai.

14. Tampilan Outputnya seperti berikut ini.

Kesimpulan:

Shapiro-Wilk, di dapat untuk Partisipasi dalam pemilihan ketua IPM ditinjau dari Kepercayaan pada calon ketua nilai probabilitas di atas 0,05 yaitu 0,274. Karena nilai signifikasi 0,274 > 0,05 maka dapat disimpulkan bahwa data berdistribusi normal.